今天要來介紹的是一個可以當做進出場訊號的指標:波動率通道。
有許多方法會被用來衡量波動率,常見的像是ATR(平均真實區間),如果波動率高,ATR就會變大。今天我們使用的觀念則是用典型價,即最高價,最低價,收盤價這三個價位的平均,拿來和最低點比較,如果典型價上漲,就用今天典型價減去昨低,反之則用昨天典型價減今低。使用這個差值,來繪製一個波動率通道,然後用這個通到的上下緣來當做買賣訊號。
腳本如下:
variable: avg(8),vperiod(13),devfact(3.55),LbandAdj(0.9);
variable:DevHigh(0),DevLow(0);
variable:aTypical(0),dev(0),medianavg(0),typ(0),XMA(0);
if currentbar>=2 then begin{必需要2根K 才能開始}
typ = typicalprice;
{典型價}
aTypical = iff(typ >typ[1],typ-Low[1],typ[1]-Low);
{IFF 第1個是判斷式,如果成立了,用第1個算式的結果,不然就用第2個算式的結果}
dev = devfact*average(atypical,vperiod);
{計算平均值的3.55倍做為通道基值}
DevHigh =Xaverage(dev,avg);
DevLow =DevHigh *LbandAdj;
{計算通道上緣與下緣的邊界}
medianavg = Xaverage(typ,avg);
XMA = Xaverage(medianavg,avg);
{用指數平均兩次平滑典型價}
plot1(XMA+DevHigh,"多方線");
plot2(XMA-DevLow,"空方線");
plot3(XMA,"中線");
{畫出通道圖}
end;
{如果需要在圖上標記買賣訊號,可以加下列}
if C cross over XMA + DevHigh then
begin {以下繪點}
plot4(C*1.01,"多");plot5(C*1.02,"多");plot6(C*1.03,"多");
plot7(C*1.04,"多");plot8(C*1.05,"多");plot9(C*1.06,"多");
plot10(C*1.07,"多");
end;
if C cross under XMA -DevLow then
begin {以下繪點}
plot11(C*0.99,"空");plot12(C*0.98,"空");plot13(C*0.97,"空");
plot14(C*0.96,"空");plot15(C*0.95,"空");plot16(C*0.94,"空");
plot17(C*0.93,"空");
end;
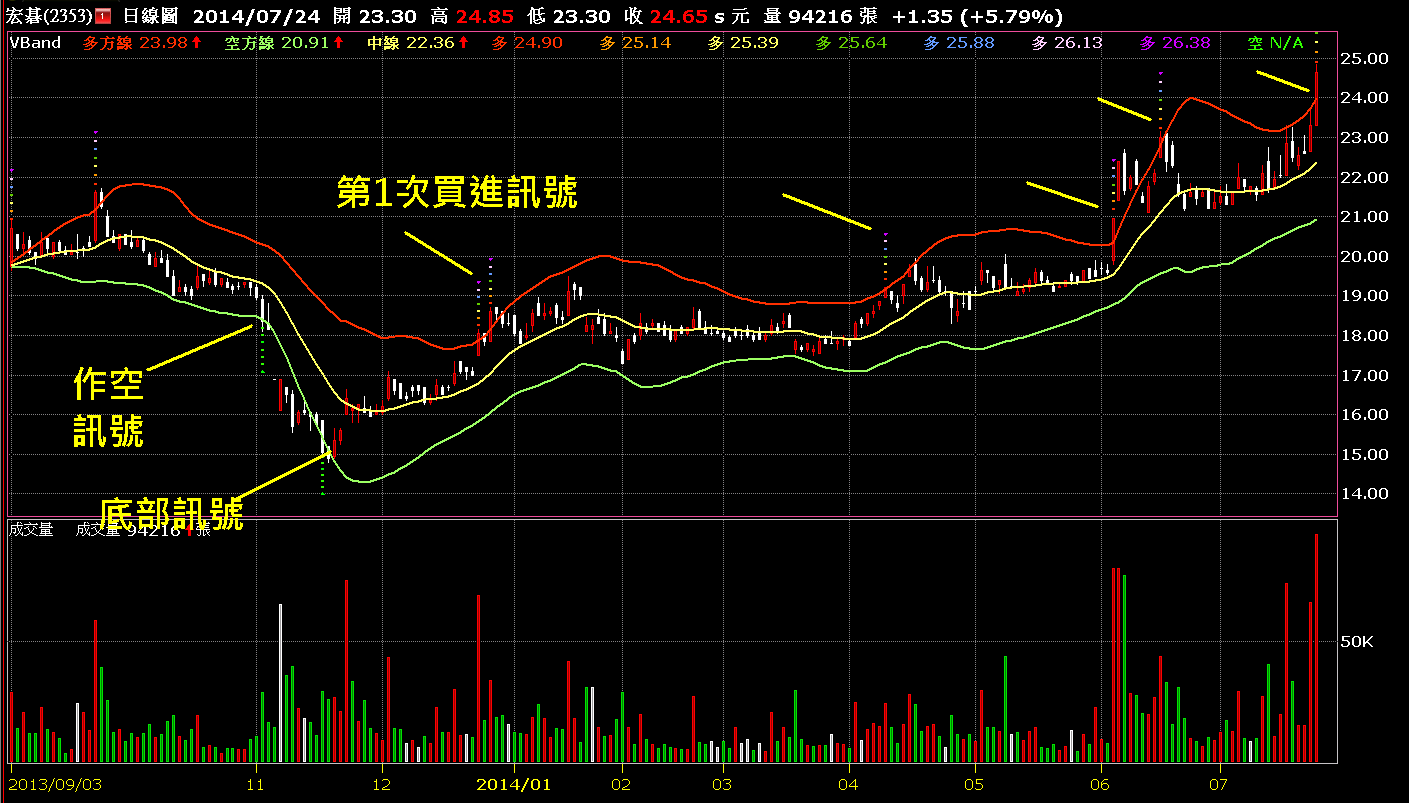
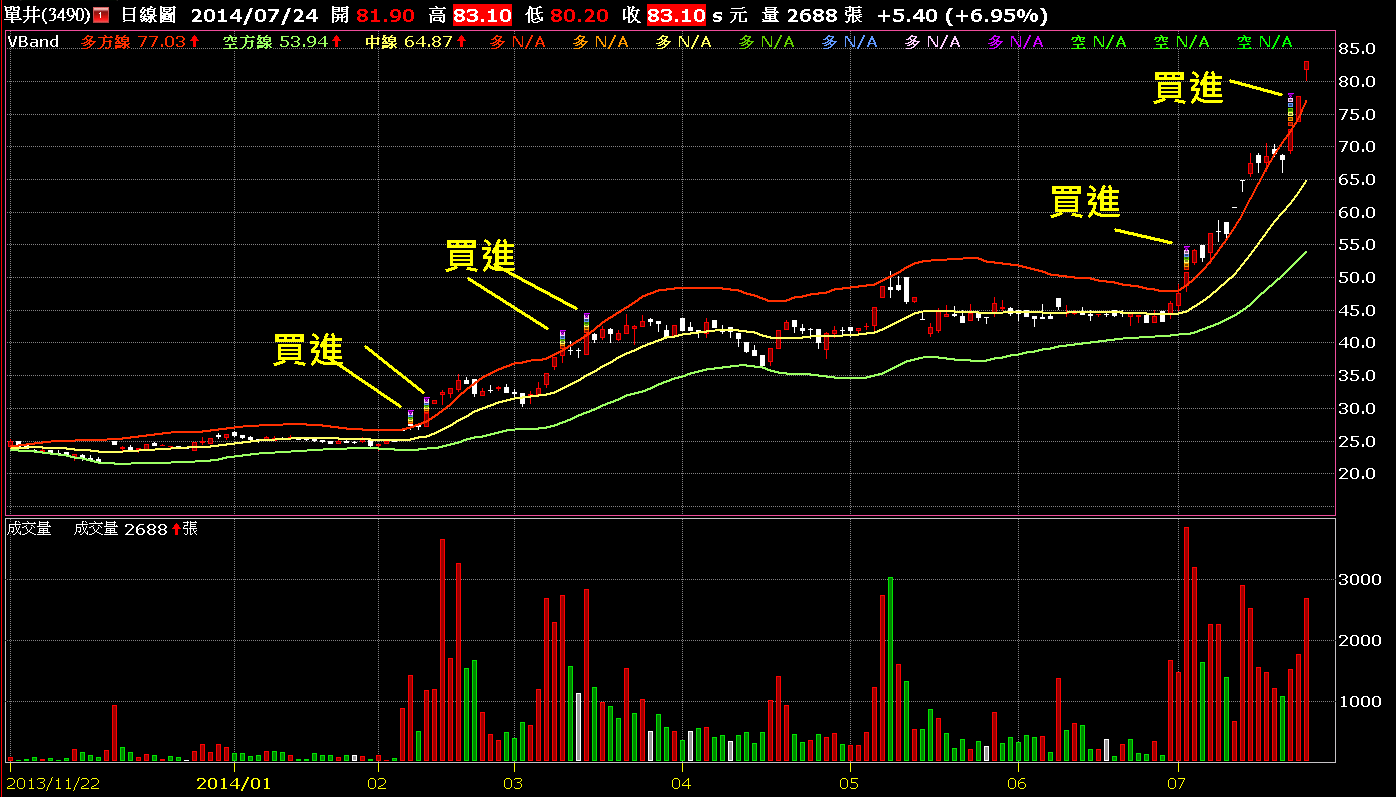
如果價格突破了通道上緣,可以標示出做多訊號,跌破通道下緣,則為做空訊號!
這個通道還有另一個觀察點:如果股價從跌破下緣後往下探低一段,接著準備上漲突破通道下緣時,是相對低點或底部區的機會就很高了,反之則可能是頭部區的形成!
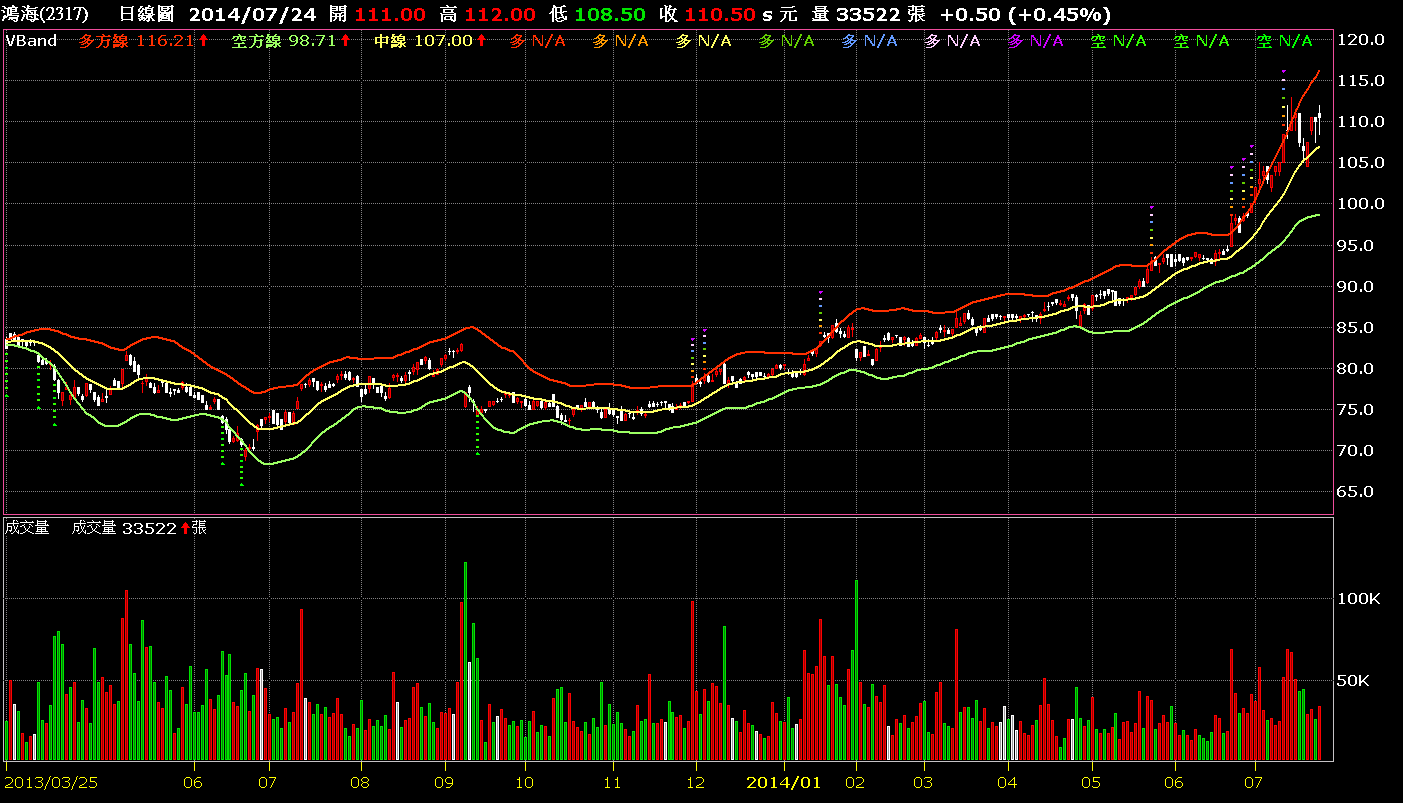
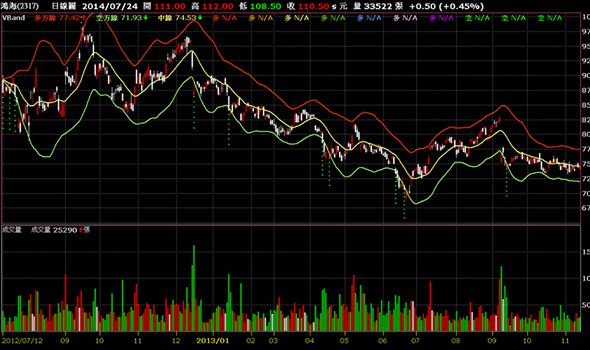
我們找了幾檔指標股來看,2317,圖上用多色垂直柱線標註了多方點,綠色柱線則是空點,從2012年12月跌破通道以來,一直都是空方格局,直到2013年11月29日出現了第1個多方點,之後一直都是多方訊號,這樣就表示了是一個很強力的多頭走勢,多方的波動率一直在放大,股價也從79元一路上漲到110元!
這樣的波動率判別不會受到公司股本市值大小的影響而有所不同,唯一的差別就是漲升的幅度而已!
各位可以試看看,如果要做成即時的警示,可以用下面的版本
variable: avg(8),vperiod(13),devfact(3.55),LbandAdj(0.9);
variable:DevHigh(0),DevLow(0);
variable:aTypical(0),dev(0),medianavg(0),typ(0),XMA(0);
if currentbar typ = typicalprice();
aTypical = iff(typ >typ[1],typ-Low[1],typ[1]-Low);
dev = devfact*average(atypical,vperiod);
DevHigh =Xaverage(dev,avg);
DevLow =DevHigh *LbandAdj;
medianavg = Xaverage(typ,avg);
XMA = Xaverage(medianavg,avg);
if C cross over XMA + DevHigh then ret=1; {多方}
上面的那個XQ頁面,有興趣的朋友可以在下面的連結中打開:
檔案連結